Characterization

PDF:

f (x; α, β) = 1 B ( α , β ) x α - 1 (1 - x) β - 1

$f(x;\alpha,\beta) = \frac{1}{\mathrm{B}(\alpha,\beta)} x^{\alpha-1}(1-x)^{\beta-1}$

B(α,β) $\mathrm {B} (\alpha ,\beta )$ is called a Beta function, and is just a normalization constant.

B (α, β) = \int 10 t α - 1 (1 - t) β - 1 d t = Γ ( α ) Γ ( β ) Γ ( α + β )

$\mathrm {B} (\alpha ,\beta )={\int_0^1 t^{\alpha-1} (1-t)^{\beta-1}\, dt}= {\frac {\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}}$

Γ(x) $\Gamma(x)$ is a gamma function.
Its general CDF function does not have an analytic expression.

Applications

Beta Distribution is the conjugate prior of many discrete distributions, including the Bernoulli and binomial distribution, in Bayesian inference.
The parameters, $\alpha$ and $\beta$ , can be intuitively interpreted as positive and negative "psudo samples". The posterior hyperparameters of Bernoulli likelihood are simply $\alpha +\sum _{i=1}^{n}x_{i},\,\beta +n-\sum _{i=1}^{n}x_{i}\!$ .

Properties

mode

Mode, in statistics, is the value that appears most often in a set of data, corresponding to the peak in the PDF. The anti-mode is the lowest point of the probability density curve.

The mode of a Beta distributed random variable X with α, β > 1 (and anti-mode with α, β < 1), is

α - 1 α + β - 2

$\frac{\alpha-1}{\alpha+\beta-2}$

mean

μ = E [X] = α α + β

$\mu = \operatorname{E}[X] = \frac{\alpha}{\alpha + \beta}$

Reference

Beta Distribution: https://en.wikipedia.org/wiki/Beta_distribution

The followings are the illustrations of the hyperparameters.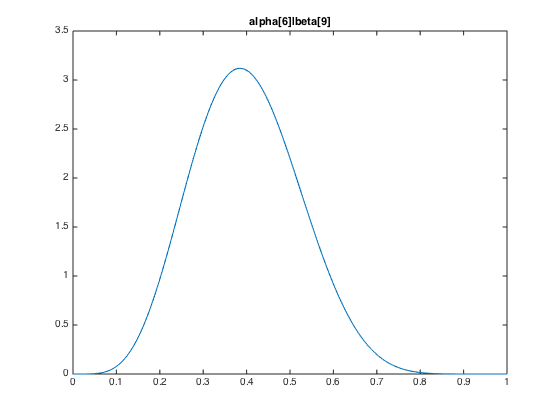

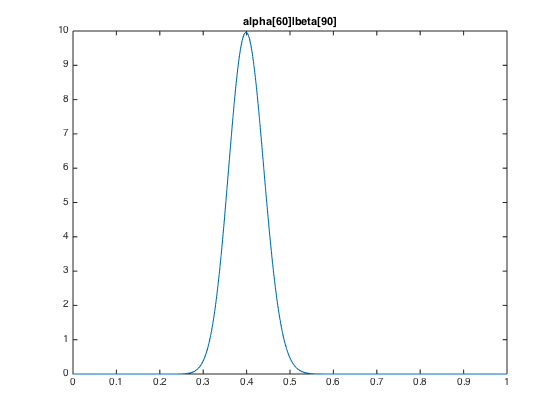
Note that y axis stands for probability density, which can exceed 1 with no surprise (probability is the integral of probability density).